Article History Submitted 2 November 2023. Accepted 10 January 2024. Keywords natural language processing, legal language, judicial reasoning, judicial behavior, embeddings |
Abstract Judicial documents and judgments are a rich source of information about legal cases, litigants, and judicial decision-makers. Natural language processing (NLP) based approaches have recently received much attention for their ability to decipher implicit information from text. NLP researchers have successfully developed data-driven representations of text using dense vectors that encode the relations between those objects. In this study, we explore the application of the Doc2Vec model to legal language to understand judicial reasoning and identify implicit patterns in judgments and judges. In an application to federal appellate courts, we show that these vectors encode information that distinguishes courts in time and legal topics. We use Doc2Vec document embeddings to study the patterns and train a classifier model to predict cases with a high chance of being appealed at the Supreme Court of the United States (SCOTUS). There are no existing benchmarks, and we present the first results at this task at scale. Furthermore, we analyze generic writing/judgment patterns of prominent judges using deep learning-based autoencoder models. Overall, we observe that Doc2Vec document embeddings capture important legal information and are helpful in downstream tasks. |
|---|
In general, legal language is complex. Words are the essential tools of the law and have great importance; cases are decided based on the meanings judges ascribe to words, and attorneys must use the right words to sway the outcome to their side. However, do machines consider legal text differently?
Law is embedded in language. In this paper, we ask what can be gained by applying new techniques from natural language processing (NLP) to the law. NLP translates words and documents into vectors within a high-dimensional Euclidean space. Vector representations of words and documents are information-dense in the sense of retaining information about semantic content and meaning, while also being computationally tractable. This combination of information density and computational tractability opens a wide realm of potentiality for mathematical tools to generate quantitative and empirically testable insights into the law.
This new approach to legal studies addresses shortcomings of existing methods for studying legal language. Because law consists of text, research methods based on formal math and numerical data are limited by the questions that can be asked. The formal theory literature has approached the law metaphorically. This case-space literature, in particular, treats the law spatially, where the law separates the fact space into ‘liable’ and ‘not liable’ or ‘guilty’ and ‘not guilty’. Case-space models give us some intuition into the legal reasoning process. But they have been somewhat limited empirically because it has been infeasible to measure the legal case space. The traditional empirical legal studies literature has relied on small-scale data sets, where legal variables are manually coded (e.g. Songer and Haire, 1992).
Machine learning (ML) is the science of training computers to act without being explicitly programmed (Tiwari 2018). Mathematical algorithms are used to identify patterns in data and become cognizant of underlying behaviors. Deep learning (DL) is a part of the broader family of Artificial Intelligence, which uses volumes of data to obtain a powerful representation of data. ML involves training computers to learn from data and make predictions, while DL uses artificial neural networks to automatically discover data representations (Alaskar 2021). Researchers have come a long way in developing powerful methodologies that can understand tabular data, audio, images, videos, and text. One of the limitations of these techniques is that they are only as good as the data (distribution) they are being trained on and fail to predict otherwise.
There have been multiple breakthroughs in computational linguistics and one significant achievement is to represent text as vectors (Blei, 2012; Mikolov et al., 2013; Jurafsky and Martin, 2014). These vectors are not random but trained in such a way that they contain important information about the word/text. For example, the success of Google's Word2Vec algorithm is that it learns the conceptual relations between words; a trained model can produce synonyms, antonyms, and analogies for any given word (Mikolov et al., 2013; Levy et al., 2015). These “word embeddings”, as the word vectors have come to be called, serve well as features in downstream prediction tasks by encoding a good deal of information in relatively rare word features. More recently, document embeddings have built upon the success of word embeddings to represent words and documents in joint geometric space (Le and Mikolov, 2014). Like word embeddings, these document embeddings have advantages in terms of interpretability and serve well in prediction and classification tasks.
In this study, we address the potential of using document embedding analysis to understand the basic tenets of legal decision-making. More specifically, we study the patterns of judgments made in the US Circuit Courts. We also demonstrate and discuss the possibilities of NLP techniques for
Automatically predicting the chance of review by the Supreme Court using ML
Identifying atypical judgements/writing patterns by judges using deep learning techniques
The rest of the paper is organized as follows. Section 2 presents related work. Section 3 describes the data and limitations. In Section 4 we discuss the proposed methodologies. Section 5 details the experiments, results, and interpretations. Finally, Section 6 concludes.
Many researchers have devoted considerable effort to using NLP on legal texts over the past few decades. Early works (Kort, 1957; Ulmer, 1963; Nagel, 1963; Segal, 1984; Gardner, 1984) used hand-crafted rules or features due to computational limitations at the time. In recent years, with rapid developments in deep learning, researchers began to apply such techniques to multiple domains. An active literature in computational legal studies has begun to apply these methods to legal documents. Livermore et al. (2016) use a topic model to understand agenda formation on the U.S. Supreme Court (see also Carlson et al., 2015). Leibon et al. (2018) use a network model to represent the geometric relations between U.S. Supreme Court cases. The authors apply a framework where legal sources are connected based on citation information and textual similarity, which is quantified using topic models. This representation leads to the creation of a natural notion of distance within the corpus, reflecting how easily a legal practitioner can navigate from one source to another. The model also allows for the identification of regions within the law that are closely related and others that are more isolated. Ganglmair and Wardlaw (2017) apply a topic model to debt contracts, while Ash et al. (2018b) apply one to labor union contracts. Legal Judgment Prediction has been studied extensively by Aletras et al. (2016); Luo et al. (2017); Zhong et al. (2018); Chen et al. (2019). Dunn et al. (2017) use ML to predict outcomes of asylum adjudication. Ye et. al. (2018) proposed a seq2seq model to generate a court view from fact descriptions of the case. This paper introduces a novel approach to generating “court views” – judicial rationales explaining charge decisions in criminal cases – using a label-conditioned sequence-to-sequence (Seq2Seq) model with attention. The concept of a “court view” is crucial in legal documents as it contains the rationale supporting the charge, helping to interpret and justify the charge decision. The authors address the challenge of generating these rationales from fact descriptions in criminal cases, a task not adequately covered by existing legal assistant systems. Their method, which incorporates charge labels to improve the distinctiveness of the generated rationales, demonstrates effectiveness in creating more interpretable and discriminative court views, particularly useful for automatic legal document generation and enhancing the functionality of charge prediction systems. Other applications of NLP in the legal domain are Legal Entity Recognition and Classification (Cardellino et al., 2017; Angelidis et al., 2018), Legal Question Answering (Monroy et al., 2009; Taniguchi and Kano, 2016; Kim and Goebel, 2017), Legal Summarization (Hachey and Grover, 2006; Bhattacharya et al., 2019). Chalkidis and Kampas (2019) trained a Word2Vec model on a large corpora of legal text comprising legislation from the UK, EU, Canada, Australia, USA, and Japan. In many NLP tasks such as text classification, sentiment analysis, and automated translation, the distributed document representation learned by the Doc2Vec model proved to outperform other techniques for text representation (Lilleberg et al 2015; Park 2019).
Autoencoders are an unsupervised learning technique that leverage neural networks for the task of representation learning. Specifically, we design a neural network architecture to impose a bottleneck in the network that forces a compressed knowledge representation of the original input. Autoencoders have been extensively applied to image data, especially for recommendation systems, anomaly detection, and image compression. Chen and Zaki (2017) developed KATE, a novel architecture to represent text using autoencoders. In the literature, there is a noticeable scarcity of research studies that explore the application of autoencoders to text data. Briciu et. al. (2022) applied autoencoder models for authorship attribution. In this study, we developed an autoencoder model to understand judge characteristics and identify atypical judgments.
The focus of this study is the U.S. Circuit Courts of Appeals, which form a critical part of the American federal judiciary. There are 12 Circuit Courts in the United States, each covering a specific geographic region encompassing 3–9 states. These courts are pivotal as they review appeals from District Courts and make rulings on the application of federal law. Their decisions have a significant influence on legal precedent, decision-making, and policy within their jurisdiction.
Each Circuit Court is composed of a varying number of judges, ranging from 8 to 40, depending on the circuit. These judges, collectively referred to as the pool of judges, are appointed by the U.S. President and confirmed by the U.S. Senate. In this system, a panel of three judges, selected from the pool, is assigned to each case. This panel operates without a jury and is responsible for delivering a binary verdict—either affirming or overturning the decision of the lower court. To decide on a verdict, a majority of two out of the three judges is required. Additionally, the panel produces a written opinion to justify their verdict, which then serves as a precedent for future cases.
In this study, we use case texts from the U.S. Appellate Circuit Courts for the years 1970 through 2013. We have detailed metadata for each case; we primarily use the court, date, case topic, authoring judge, jury, and whether the case was appealed at the Supreme Court for reversal. For case topics, we use the 7- category “General Issue” designation coded for Donald Songer's Court of Appeals Database. The cases are linked to biographical information on the judges obtained from the Federal Judicial Center. This includes the birth date, gender, and political affiliation of appointing president. Overall, the dataset contains 380,253 case texts spanning twelve circuit courts across the US. These judgments covered a total of around 80 different topics.
In this study, the use of metadata plays a crucial role in enhancing the depth and validity of our analysis. Metadata, including information such as the court, date, case topic, authoring judge, jury presence, and appeal status at the Supreme Court, provides essential contextual dimensions to the case texts. For instance, incorporating the authoring judge's metadata allows us to link the textual patterns in judgments with specific judicial decision-making styles. Similarly, the appeal status at the Supreme Court, a key dependent variable for our first research question, offers a direct measure to evaluate the predictive power of our models in forecasting case outcomes. The inclusion of such multidimensional data not only bolsters the robustness of our findings but also opens avenues for subsequent legal analyses.
The original dataset was obtained in HTML format. Each case was a single HTML file and they contained all the case-related information such as Plaintiff-Appellant, appellee, the jury of judges, case filed to date, argument, and submission date, and the opinions of one or more judges. They also contain other irrelevant information such as markups, citations, hyperlinks, etc.
The following steps were followed to clean the dataset for modeling.
The top and bottom parts of the HTML page contained hyperlinks, index information, etc. The first step involved extensive cleaning of the data to remove all unnecessary information.
The first few lines of the cleaned data contain high-level information about the case, such as the court, judge, and date. Using Regular Expression (Regex) we extract relevant metadata information.
After extracting the metadata, we use fuzzy name-matching algorithms to clean the judge names.
Each case contains either one concurring major opinion or partially concurring and dissenting opinions from the jury members. Each opinion is expressed by one or more judges in the panel and together they provide a direction to the outcome of the case. We use HTML tags and Regex to identify individual opinions and tag them to the corresponding judge. If multiple judges concur on the same opinion, we tag the same opinion with all the judges. This way we obtain the directional opinion of each judge, and this is used to obtain individual judge characteristics (discussed in detail in Section 4).
In this process, we exclude cases where the case text had either partial or no information about the case or missed relevant information for the outcomes. We filtered the data based on topics to ensure we had ample case text for each topic. The distribution is as follows.

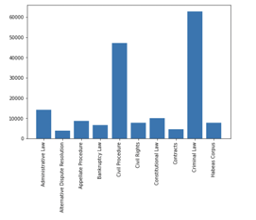
Figure 1. Distribution of Case Topics Post-Data Cleaning. The bar graph illustrates the distribution of case topics remaining after the data cleaning process from the original HTML dataset, spanning from 1970 to 2013. The data cleaning involved the removal of irrelevant markup, hyperlinks, and extraneous information, extraction of metadata using Regex, normalization of judge names through fuzzy matching, and tagging of individual and concurring opinions to corresponding judges. The final dataset comprises 173,291 cases with 197,487 distinct opinions, which were then split into training and testing sets for model development. The cases are categorized by topic, indicating the volume of available text for each subject area.
After the data cleaning process, we had 173,291 cases, and these had in total 197,487 individual/concurring opinions for the period 1970–2013. We experimented with two train-test splits.
Randomly split the data into 80-20 splits for training-testing respectively
Use data from 1970–2005 for training and >2005 for testing
Word2Vec was proposed as an efficient neural approach to learning high-quality embeddings for words (Mikolov et al., 2013a). The model was trained to predict a word given its context. The objective function of Word2Vec is to maximize the log probability of context word (\(w_{o}\)) given its input word (\(w_{i}\)), i.e. log P(\(w_{o}\)|\(w_{i}\)). One advance was to combine the above objective with negative sampling in order to maximize the dot product of the \(w_{i}\) and \(w_{o}\) while minimizing the dot product of \(w_{i}\) and randomly sampled “negative” words.
\[\log log\ \sigma\left( {v_{w_{o}}^{'}}^{T}v_{w_{I}} \right)\ + \ \sum_{i}^{k}{}w_{i}\sim P_{n}(w)\left\lbrack \log log\ \sigma\ ( - {v_{w_{i}}^{'}}^{T}v_{w_{I}} \right\rbrack\]
Where \(\sigma\) is the sigmoid function, \(k\) is the number of negative samples, \(P_{n}(w)\) is the noise distribution, \(v_{w}\) is the vector of word \(w\) and \(v_{w}^{'}\) is the negative sample vector of the word \(w\).
There are two approaches in Word2Vec namely Skip-Gram (SG) and Continuous Bag-of-Words (CBOW). In SG, the input is a word and the output is a context word. For each input word, the number of left or right context words to predict is defined by the window size hyperparameter. CBOW is different from skip-gram in one aspect: the input consists of multiple words that are combined via vector addition to predict the context word.
To illustrate, a word embedding can identify similar words in the vocabulary. For example, “judge” might be close to “jury” but far away from “flowerpot”. Similarly, a document embedding can identify similar cases in a corpus of decisions based on use of similar language. For example, Engel v. Vitale (1962) might be spatially close to Everson v. Board of Education (1947), since they are both early U.S. Supreme Court decisions that deal with religious freedoms in the US.
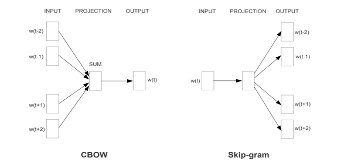
Figure 2. Word2Vec Model Architectures. This figure presents the two primary architectures of the Word2Vec model: Skip-Gram (SG) and Continuous Bag-of-Words (CBOW). In the SG model, the process begins with a target word and predicts the surrounding context words, while the CBOW model takes multiple context words to predict a target word. The central concept is to use word vectors and optimize their positions such that words with similar context are located closer in the vector space, allowing for the capture of semantic and syntactic word relationships.
Le and Mikolov, in 2014, developed a similar version of embeddings for documents called Doc2Vec. There are two approaches within Doc2Vec, namely, Distributed Bag-of-Words (DBOW) and Distributed Memory Paragraph Vectors (DMPV). DBOW works in the same way as SG, except that the input is replaced by a special token representing the document. In this architecture, the order of words in the document is ignored; hence the name distributed bag of words. DMPV works in a similar way to CBOW. For the input, DMPV introduces an additional document token along with multiple target words. Unlike CBOW, however, these vectors are not summed but concatenated. The objective is to predict a context word given the concatenated document and word vectors.
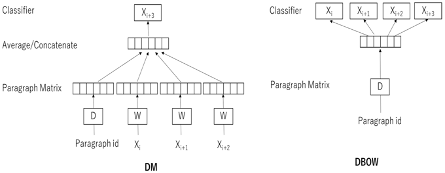
Figure 3. Doc2Vec Model Architectures. Illustrated here are the two architectures within the Doc2Vec framework: Distributed Bag-of-Words (DBOW) and Distributed Memory Paragraph Vectors (DMPV). DBOW mirrors the SG model of Word2Vec but uses a document token as input to predict words in the document, disregarding word order. DMPV is analogous to the CBOW model, combining a document token with words to predict the next word in the text. Both methods aim to create document vectors that encapsulate the essence of the document, enabling the identification of documents with similar themes or content.
Once we train the Doc2Vec model, we have vector i for each opinion. Each case has an authoring judge j, working in court c at year t. Besides author and time, the other metadata feature is the case topic k. We compute the case vector by computing the average of all opinion vectors.
\[C_{t} = \frac{1}{{|I}_{j}|}\sum_{i \in I_{j}}^{}{}i\]
Where |.| gives the count of the set. Similarly, the vector for the judge j at year t would be given by
\[J_{t} = \frac{1}{{|I}_{j_{t}}|}\sum_{i \in I_{j_{t}}}^{}{}i\]
And the vector for judge j, case topic k and year t would be computed as
\[J_{kt} = \frac{1}{{|I}_{j_{kt}}|}\sum_{i \in I_{j_{kt}}}^{}{}i\]
Once we compute, the case vector \(C_{t}\), judge_year \(J_{t}\) and judge_topic_year \(J_{kt}\) vector, we present a variety of visualizations to understand better the spatial relationships encoded by our case vectors and judge vectors. We use t-SNE plot (Maaten and Hinton, 2008), which projects the vectors down to two dimensions for visualization purposes. We use t-SNE plots, rather than principal components, because the dimension reduction algorithm is designed to project data while preserving relative distance between points. The dots represent vectors, and the colors/labels represent groupings. Finally, we develop XGBoost based ML models on case vectors to predict chances of appeal at the Supreme Court. We present a detailed comparison of results in Section 5.
Autoencoders utilize an unsupervised learning approach, employing neural networks to facilitate representation learning. The structure is intentionally designed with a bottleneck, compelling the network to generate a condensed knowledge representation of the initial input. Additionally, if the input data has patterns, compression helps in identifying implicit structure in the data and leveraging this information to identify anomalous decisions, low-level representation, noise removal, etc.
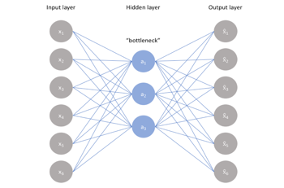
Figure 4. Architectural Diagram of an Autoencoder. This figure illustrates the architecture of an autoencoder neural network used in the study to analyze individual judge characteristics and behavior. The network is constructed with an input layer, a hidden layer that forms a "bottleneck," and an output layer. The bottleneck forces a compressed representation of the input data, enabling the model to capture essential features and discern underlying patterns. Through this process, the autoencoder aids in identifying unique or anomalous decisions, extracting low-level representations, and removing noise from the dataset, which is pivotal in understanding and predicting judicial decision-making behaviors.
In this study, we use autoencoder models to study individual judge characteristics, understand their general behavior and identify atypical judgements.
Doc2Vec training operates entirely without supervision; that is, it processes only the raw text without relying on any supervised or annotated data. We utilized the opinion texts from section 3.3 as training data for developing the model. The model's effectiveness is then assessed using test data in two main areas: (i) similarity analysis involving cases, opinions, and judges, and (ii) predicting the likelihood of an appeal. For similarity analysis, the model examines how closely related different legal documents are based on their content. ’Case similarity’ involves comparing different legal cases to identify commonalities in facts, legal issues, or decisions. ‘Opinion similarity’ focuses on analyzing the text of judicial opinions to find parallels in reasoning, language, or legal principles. ‘Judge similarity’ assesses how similar the decisions or opinions of different judges are, which could indicate shared judicial philosophies or interpretative approaches. Furthermore, the model's ability to predict the chance of an appeal is tested, determining how likely a case is to be appealed based on its characteristics. This evaluation involves extensive hyperparameter tuning using various options available in gensim, a Python package that implements the Doc2Vec model.
Objective: distributed bag-of-words (DBOW) model, distributed memory (DM) model
Embedding Vector Size: 50, 100, 200 and 300
Train (or not train) word-vectors (in SG fashion) simultaneous with DBOW doc-vector training
Context Window Size: 5, 10, 20
Learning rate: 0.025, 0.05, 0.1
Additionally, gensim has the option of passing in tags, which can be used as an identifier of the text and the Doc2Vec generates trained vectors for these tags. During testing, we infer the vectors using gensim’s inbuilt function (infer_vector).
We train the Doc2Vec models and evaluate them on
Ability to capture the expected patterns in text and review the same with subject matter experts.
SCOTUS Chance of Appeal Prediction task
In this section we present a variety of visualizations to understand better the spatial relationships encoded by our case vectors and judge vectors. We use t-Distributed Stochastic Neighbor Embedding (t-SNE), a technique for dimensionality reduction that is particularly well suited for the visualization of high-dimensional datasets.
t-Distributed Stochastic Neighbor Embedding (t-SNE) is an advanced machine learning algorithm particularly useful for visualizing high-dimensional data. It operates by first computing the pairwise similarity between data points in the high-dimensional space, using a Gaussian distribution to model this similarity. This process essentially measures how ‘close’ or ‘similar’ data points are to each other based on their features, which in the context of legal documents could be aspects like citation patterns, textual content, or thematic elements. t-SNE then aims to map these high-dimensional data points into a two-dimensional space in such a way that similar points are placed near each other and dissimilar points are placed apart. This mapping is achieved through a series of iterations, where the algorithm optimizes the positions of points using a t-distribution, which is particularly effective at managing the crowding problem inherent in reducing dimensions. In the resulting two-dimensional representation, the spatial distance between any two points reflects their relative similarity: a shorter distance implies greater similarity, making it a powerful tool for uncovering inherent structures or clusters within complex datasets, such as a large corpus of legal documents.
We begin by exploring the institutional, temporal and judge level features encoded in the vectors. For Figure 5, we plot the plain Doc2Vec vectors from the corpus. We observe that there exists a temporal pattern across years; additionally the topics are congregated in some pattern, clearly exhibiting a structure in the learned Doc2Vec models.
For Figure 6, we centered the case vectors by topic interacted with year, as described above. We then averaged by judge and plotted the judge vectors. We observe that the Doc2vec model is well able to capture the general characteristics of the topic.

Figure 5. T-SNE of document embeddings without centering
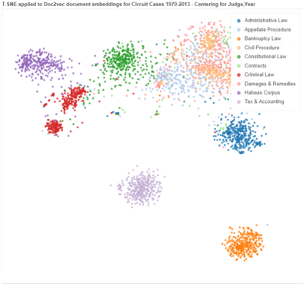
Figure 6. T-SNE of document embeddings centering for Judge and Year
The linguistic and reasoning styles of judges are foundational to the body of legal jurisprudence. In this section, we focus on representing judges as vectors to establish a similarity metric between judges, enabling us to conduct an in-depth, large-scale exploration of their linguistic ties. We adopt a measure of vector similarity that is used often for document classification. The cosine similarity between vectors is given by
\[s\left( \overrightarrow{v},\overrightarrow{w} \right) = \ \frac{\overrightarrow{v}.\overrightarrow{w}}{\|\overrightarrow{v}\|\|\overrightarrow{w}\|}\]
which is equal to 1 minus the cosine of the angle between the vectors. It takes a value between -1 and 1. In the case of judges, similarities approaching 1 mean that judges tend to use similar language in their opinions. Similarities approaching -1 mean the judges rarely use the same language. In Figure 7 we plot the similarities of judges for whom we have the largest number of opinions. The colors provide a gradient for similarity. We find that judge pairs with high scores exhibit a lot of similarity in their judgment patterns. For example, looking at Richard A Posner, a notable judge who is known for his economic analysis in opinions, there is a high similarity with Frank Easterbrook, who also presents his opinions with an economic standpoint. We validated these comparisons with subject matter experts.
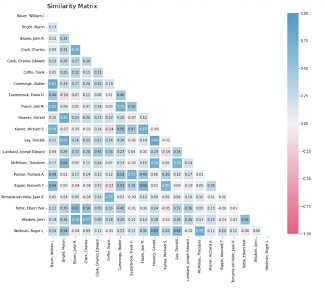
Figure 7. Correlation heatmap of top judges
In the preceding sections of this paper, our exploration has utilized Natural Language Processing (NLP) methodologies to construct a quantifiable framework for ‘mapping the geometry of law’. Building upon this foundation, we now extend our exploration to a critical dimension of judicial activity: the voting patterns of judges. The objective here is to synthesize the insights derived from our NLP-based exploration of legal texts with the empirical patterns evident in judicial decision-making. This investigation focuses on the alignment and divergence in judicial voting behaviors, thereby validating our geometric mapping of legal reasoning with the dynamics of judicial collaboration and individuality.
To quantify these interactions, we analyze ‘Judge Voting Similarity’ across approximately 380,000 cases. This similarity is calculated as the percentage of instances where judges voted the same way out of the total occasions they served together on a panel. The formula for Judge Voting Similarity (%) is thus:
\[Judge\ voting\ Similarity\ (\%) = \ \frac{number\ of\ times\ voted\ together\ }{number\ of\ times\ sat\ together}\]
In order to validate and deepen our understanding of these voting patterns, we employ a weighted least square regression. This method correlates the judge voting similarity with the linguistic similarity between their written opinions, as determined by our Doc2Vec model. The weighting in the regression is particularly crucial as it factors in the frequency of judges sitting together, effectively minimizing any skewing effects due to the presence of visiting judges or variations in panel composition. The regression's results are presented visually through binscatter plots, offering a clear and interpretable representation of the relationship between linguistic alignment in judicial opinions and actual voting concordance.
| Table 1. Correlation of Judicial Voting and Linguistic Similarity. | |
|---|---|
| (1) Judge voting Similarity |
|
| Correlation based on Doc2vec | 0.0216*** (0.00393) |
| Intercept | 0.930*** (0.00245) |
| Observations | 9634 |
| R-sq | 0.003 |
| Note: This table reports the results of a weighted least square regression analysis examining the relationship between Judge Voting Similarity and linguistic similarity of written opinions as determined by a Doc2Vec model. The dependent variable, Judge Voting Similarity, is calculated as the proportion of times judges vote in concordance when serving on the same panel. The key independent variable is the correlation of judges’ opinions based on Doc2Vec vector representations, indicating linguistic similarity. The regression is weighted by the frequency of judges sitting together to account for variations in panel compositions and to mitigate potential biases from visiting judges. Standard errors are provided in parentheses, with significance levels denoted by asterisks (*p<0.1, ** p<0.05, *** p<0.01). | |
We observe that there exists a positive relationship between the correlation obtained from the Doc2Vec model and the vote-together similarity scores. This indicates that Doc2Vec has been successful enough to capture the important judge-level characteristics.
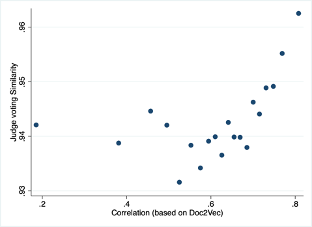
Figure 8. Binscatter Plot of Judicial Voting Similarity vs. Linguistic Similarity. This figure illustrates a binscatter plot that visualizes the relationship between Judge Voting Similarity and the linguistic similarity of judges' written opinions as captured by the Doc2Vec model. Each bin represents an aggregation of case points, reflecting the proportion of aligned votes between judges against their opinions’ linguistic correlation. The positive slope indicates a discernible trend where linguistic resemblance is associated with higher instances of voting concordance.
We also plot the binned scatter plot and we observe the positive relationship between the vote together percentage and correlation.
The Circuit Court decision is usually the final word in the case, unless it sends the case back to the trial court for additional proceedings, or the parties ask the Supreme Court to review the case. In some cases the decision may be reviewed en banc, that is, by a larger group of judges (usually all) from the circuit. Historically, 25% of Circuit Court cases are appealed to the Supreme Court but only 3% of those cases are heard in the Supreme Court. Understanding that the U.S. Supreme Court (SCOTUS) only hears a small fraction of the cases appealed from Circuit Courts, our objective was to predict which cases are more likely to be heard by SCOTUS. This prediction is crucial as it guides legal professionals to focus their resources effectively, considering that each case preparation demands significant effort, time, and expense.
The dataset we used reflects the real-world scenario where only a small percentage of appealed cases are heard by SCOTUS, creating a highly imbalanced dataset with a ratio of 99:1 (not heard vs. heard). This imbalance presents a unique challenge: standard models may be biased towards predicting that cases will not be heard, as this is the more common outcome.
To address this, we employed Doc2Vec, an algorithm that converts textual data (like legal case descriptions) into numerical vectors. These vectors capture the semantic essence of the cases in a multi-dimensional space (either 50-dimensional or 200-dimensional), effectively transforming textual information into a format suitable for machine learning models.
We split our dataset randomly into two sets: a training set and a test set. The training set is used to 'teach' the model the patterns associated with cases that SCOTUS is likely to hear. The test set, which the model hasn't seen during training, is then used to evaluate how well our model can generalize its predictions to new, unseen data.
We experimented with various machine learning models, including Logistic Regression, Random Forest, and XGBoost. Each of these models has its strengths and is known for handling classification tasks well. To fine-tune these models and select the best-performing one, we used an extensive hyperparameter tuning process. Our primary metric for evaluating model performance was the Area Under Curve (AUC) of the Receiver Operating Characteristic (ROC) curve. AUC is a robust metric for binary classification tasks, especially useful in the context of imbalanced datasets, as it measures the model's ability to discriminate between the two classes (cases heard vs. not heard by SCOTUS).
Our approach is grounded in the logic that textual characteristics of cases, when transformed into a structured, numerical format, can reveal patterns that are indicative of SCOTUS's interest in hearing certain cases. By training machine learning models on these features, we aim to capture these patterns and use them to predict future cases that SCOTUS might select to hear. In summary, our method combines advanced text representation techniques with machine learning models to predict SCOTUS case selections. This approach is novel in its application to such a vast dataset and holds significant potential for aiding legal professionals in their case preparation strategies.
Below are the results from the experiments.
| Table 2. This table outlines the comparative performance of three machine learning models in predicting the likelihood of Circuit Court cases being heard by SCOTUS. The models evaluated include Logistic Regression, Random Forest, and XGBoost. Each model's performance is measured in terms of the Area Under the Receiver Operating Characteristic Curve (AUC) for both training and testing datasets, and the F1 score for the test dataset. The AUC metric gauges the model's ability to distinguish between the binary outcomes of cases being heard versus not heard by SCOTUS, while the F1 score provides a balance between precision and recall. The Random Forest model exhibits a superior performance on the training set with an AUC of 0.80, while the XGBoost model leads in the test set with an AUC of 0.74 and the highest F1 score of 0.11, indicating its effectiveness in generalizing predictions to unseen data. | |||
|---|---|---|---|
| Model | Train AUC | Test AUC | Test F1 |
| Logistic Regression | 0.65 | 0.58 | 0.06 |
| Random Forest | 0.80 | 0.72 | 0.10 |
| XGBoost | 0.76 | 0.74 | 0.11 |
The XGBoost model yields the best results with high AUC in the test set. Since this is a highly imbalanced dataset, we observe a little lower performance in other metrics. We generate the gain chart to further analyze the prediction power of the model.
| Table 3. This gain chart illustrates the effectiveness of the XGBoost model in predicting the likelihood of cases being selected by the Supreme Court. The chart is divided into deciles, showing in each decile the count of cases, the number of cases that SCOTUS accepted, the cumulative number of cases that SCOTUS accepted, the percentage of total accepted cases in each decile, and the gain (a measure of effectiveness of classification) and lift (how much a model is better than random guessing) for each decile. It highlights the model's accuracy in identifying cases with a higher probability of being heard by SCOTUS, particularly in the top deciles. | ||||||
|---|---|---|---|---|---|---|
| Decile group | Count cases | Scotus cert | Total Scotus Cert | Percent of Cases | Gain | Lift |
| (0.6, 0.96] | 3608 | 177 | 177 | 41.943128 | 41.943128 | 4.194313 |
| (0.5, 0.6] | 3607 | 70 | 247 | 16.587678 | 58.530806 | 2.926540 |
| (0.43, 0.5] | 3608 | 50 | 297 | 11.848341 | 70.379147 | 2.345972 |
| (0.38, 0.43] | 3607 | 44 | 341 | 10.426540 | 80.805687 | 2.020142 |
| (0.33, 0.38] | 3608 | 24 | 365 | 5.687204 | 86.492891 | 1.729858 |
| (0.3, 0.33] | 3607 | 23 | 388 | 5.450237 | 91.943128 | 1.532385 |
| (0.26, 0.3] | 3608 | 13 | 401 | 3.080569 | 95.023697 | 1.357481 |
| (0.23, 0.26] | 3607 | 8 | 409 | 1.895735 | 96.919431 | 1.211493 |
| (0.19, 0.23] | 3608 | 9 | 418 | 2.132701 | 99.052133 | 1.100579 |
| (0.02, 0.19] | 3608 | 4 | 422 | 0.947867 | 100.000000 | 1.000000 |
The model at the top decile has higher prediction accuracy, indicating that the model can identify cases that have a higher chance of getting selected by SCOTUS. While there are multiple reasons why a case gets picked up, the model can identify those patterns from the vectorized document and assign higher probabilities to those cases in the top decile.
Doc2Vec is useful in vectorizing and visualizing documents. However, we go a step further to analyze judge characteristics using the judgments they have authored. We sample a set of 10 top judges and using the document vectors of the judgments where they were a part of the judicial panel, we develop individual autoencoder models. The autoencoders were trained to reduce the mean-squared error from their reconstruction.
Once the model is trained, we estimate the similarity between the original vector and the reconstructed vector using cosine similarity. The purpose of the autoencoder model is to identify patterns or characteristics of an authoring judge and try to identify cases where the judgment is not per the expectations. Additionally, we observe a significant relationship between the similarity scores estimated from the Autoencoder model and SCOTUS Cert (the case is picked up by the Supreme Court). We use the similarity score as a measure of estimating how much a judgment text exhibits the author’s style. We control for year fixed effects so the association can be interpreted as indicating that the more anomalous or unusual is the Circuit Court writing compared to other Circuit cases in that year, the more likely the Supreme Court will decide to listen to the case.
| Table 4. Relationship Between Judicial Patterns and Supreme Court Certiorari Decisions. | |
|---|---|
| (1) Supreme Court cert |
|
| Textual Similarity | -0.0313** (0.00250) |
| Intercept | 0.0358** (0.00187) |
| Observations | 478540 |
| R-sq | 0.002 |
| Note: This table reports the results of a regression analysis estimating the relationship between the similarity of judgment texts to the authoring judge's characteristic writing style and the likelihood of the case being granted certiorari by the Supreme Court. Textual similarity is measured using cosine similarity scores between the original and reconstructed document vectors via individual autoencoder models. The negative coefficient for Textual Similarity suggests that as the Circuit Court opinions deviate more from a judge's typical writing style, the higher the probability of Supreme Court review. Standard errors are reported in parentheses with the following significance levels: *p<0.1, **p<0.05, ***p<0.01. The model controls for year fixed effects, which implies that the comparison of Circuit Court writing is made relative to other cases within the same year. The R-squared value indicates the proportion of variance in the dependent variable (Supreme Court cert) that can be predicted from the independent variable (Textual Similarity). | |
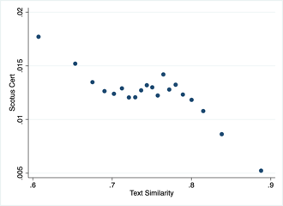
Figure 9. Binscatter Plot of Textual Similarity and Supreme Court Certiorari Decisions. This binscatter plot illustrates the relationship between the cosine similarity of judgment texts to the characteristic writing style of authoring judges and the likelihood of the cases being granted certiorari by the Supreme Court. Each bin represents an aggregate of cases, plotting the average similarity score against the proportion of cases receiving cert within that bin. The trend line provides a visual representation of the negative association between textual similarity and Supreme Court certiorari decisions, indicating that cases with judgment texts less typical of the judge's writing style are more likely to be reviewed by the Supreme Court. Observations are controlled for year fixed effects to account for temporal variations.
Our study, which applies Doc2Vec and deep learning techniques to legal texts, has several implications for legal research and practice. Firstly, by transforming complex legal documents into structured, numerical vectors, Doc2Vec enables a more nuanced analysis of judicial reasoning and patterns in judgments. This transformation is particularly valuable for legal practitioners who can now leverage these vectors to distill and comprehend vast amounts of legal texts efficiently. The vectors serve as a rich source of information, encapsulating the semantic depth of the documents, which can be instrumental in various sub-tasks such as case analysis, precedent research, and legal argumentation.
Our research also contributes to the predictive aspect of legal practice. The application of machine learning models, particularly in forecasting the probability of a case being heard by the Supreme Court, offers a strategic tool for legal professionals. By identifying the patterns and characteristics that increase the likelihood of a case being selected by SCOTUS, practitioners can better prioritize cases and allocate resources. This predictive ability is not only a testament to the power of machine learning in legal analytics but also a practical aid in decision-making processes within law firms and legal departments.
Furthermore, the use of autoencoders to analyze judge characteristics and identify outlier judgments introduces a novel dimension to understanding judicial behavior. This deep learning approach can unravel individual judge's tendencies, preferences, and unique styles, offering insights into their decision-making processes. Such information could be invaluable for lawyers in tailoring their arguments or anticipating judicial attitudes in specific cases.
In conclusion, our study demonstrates the transformative potential of NLP and machine learning in the legal field. By converting legal texts into analyzable data and employing advanced analytical techniques, we open new pathways for legal research and practice. These tools not only enhance our understanding of the law but also offer practical solutions for navigating the complex landscape of legal documents and judicial decisions.
Angelidis, Iosif, Ilias Chalkidis, and Manolis Koubarakis. "Named Entity Recognition, Linking and Generation for Greek Legislation." JURIX. 2018. https://doi.org/10.3233/978-1-61499-935-5-1
Alaskar, H. and Saba, T., 2021. Machine learning and deep learning: a comparative review. Proceedings of Integrated Intelligence Enable Networks and Computing: IIENC 2020, pp.143-150. https://doi.org/10.1007/978-981-33-6307-6_15
Aletras, Nikolaos, et al. "Predicting judicial decisions of the European Court of Human Rights: A natural language processing perspective." PeerJ Computer Science 2 (2016): e93. https://doi.org/10.7717/peerj-cs.93
Ash, E., MacLeod, W. B., and Naidu, S. (2018b). Optimal contract design in the wild: Rigidity and discretion in collective bargaining. Technical report at SSRN 3204832 (2018).
Bhattacharya, Paheli, et al. "A comparative study of summarization algorithms applied to legal case judgments." European Conference on Information Retrieval. Springer, Cham, 2019. https://doi.org/10.1007/978-3-030-15712-8_27
Blei, David M. "Probabilistic topic models." Communications of the ACM 55.4 (2012): 77-84. https://doi.org/10.1145/2133806.2133826
Cardellino, Cristian, et al. "A low-cost, high-coverage legal named entity recognizer, classifier, and linker." Proceedings of the 16th edition of the International Conference on Articial Intelligence and Law. 2017. https://doi.org/10.1145/3086512.3086514
Carlson, K., Livermore, M. A., and Rockmore, D. (2015). A quantitative analysis of writing style on the us supreme court. Wash. UL Rev., 93:1461. http://dx.doi.org/10.2139/ssrn.2554516
Chalkidis, Ilias, and Dimitrios Kampas. "Deep learning in law: early adaptation and legal word embeddings trained on large corpora." Artificial Intelligence and Law 27.2 (2019): 171-198. https://doi.org/10.1007/s10506-018-9238-9
Chen, Daniel L. "Judicial analytics and the great transformation of American Law." Artificial Intelligence and Law 27.1 (2019): 15-42. https://doi.org/10.1007/s10506-018-9237-x
Czibula, Gabriela, Mihaiela Lupea, and Anamaria Briciu. "Enhancing the Performance of Software Authorship Attribution Using an Ensemble of Deep Autoencoders." Mathematics 10.15 (2022): 2572. https://doi.org/10.3390/math10152572
Dunn, Matt, et al. "Early predictability of asylum court decisions." Proceedings of the 16th edition of the International Conference on Artificial Intelligence and Law. 2017. https://doi.org/10.1145/3086512.3086537
Garg, N., Schiebinger, L., Jurafsky, D., and Zou, J. (2018). Word embeddings quantify 100 years of gender and ethnic stereotypes. Proceedings of the National Academy of Sciences, 115(16): E3635 - E3644. https://doi.org/10.1073/pnas.1720347115
Hachey, Ben, and Claire Grover. "Extractive summarisation of legal texts." Artificial Intelligence and Law 14.4 (2006): 305-345 https://doi.org/10.1007/s10506-007-9039-z
Jurafsky, D. and Martin, J. H. (2014). Speech and language processing, volume 3. Pearson London. https://web.stanford.edu/~jurafsky/slp3/
Kim, Mi-Young, and Randy Goebel. "Two-step cascaded textual entailment for legal bar exam question answering." Proceedings of the 16th edition of the International Conference on Articial Intelligence and Law. 2017. https://doi.org/10.1145/3086512.3086550
Le, Q. and Mikolov, T. (2014). Distributed representations of sentences and documents. In Proceedings of the 31st International Conference on Machine Learning, volume 32 of Proceedings of Machine Learning Research https://proceedings.mlr.press/v32/le14.html
Leibon, G., Livermore, M., Harder, R., Riddell, A., and Rockmore, D. (2018). Bending the law: geometric tools for quantifying influence in the multinetwork of legal opinions. Artificial Intelligence and Law, 26(2):145-167. https://doi.org/10.1007/s10506-018-9224-2
Levy, O., Goldberg, Y., and Dagan, I. (2015). Improving distributional similarity with lessons learned from word embeddings. Transactions of the Association for Computational Linguistics, 3:211-225. https://doi.org/10.1162/tacl_a_00134
Lilleberg, J., Zhu, Y. and Zhang, Y., 2015, July. Support vector machines and word2vec for text classification with semantic features. In 2015 IEEE 14th International Conference on Cognitive Informatics & Cognitive Computing (ICCI* CC) (pp. 136-140). IEEE. doi: 10.1109/ICCI-CC.2015.7259377.
Livermore, M. A., Riddell, A., and Rockmore, D. (2016). Agenda formation and the us supreme court: A topic model approach. https://api.semanticscholar.org/CorpusID:155754134
Luo, Bingfeng, et al. "Learning to predict charges for criminal cases with legal basis." arXiv preprint arXiv:1707.09168 (2017).
Maaten, L. v. d. and Hinton, G. (2008). Visualizing data using t-sne. Journal of Machine Learning Research, 9(Nov):2579-2605
Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., and Dean, J. (2013). Distributed representations of words and phrases and their compositionality. In Advances in neural information processing systems, pages 3111-3119
Park, S., Lee, J. and Kim, K., 2019. Semi-supervised distributed representations of documents for sentiment analysis. Neural Networks, 119, pp.139-150. https://doi.org/10.1016/j.neunet.2019.08.001
Songer, Donald R., and Susan Haire. 1992. "Integrating Alternative Approaches to the Study of Judicial Voting: Obscenity Cases in the U.S. Courts of Appeals." American Journal of Political Science 36:963-82. https://doi.org/10.2307/2111356
Taniguchi, Ryosuke, and Yoshinobu Kano. "Legal yes/no question answering system using case-role analysis." JSAI International Symposium on Artificial Intelligence. Springer, Cham, 2016. https://doi.org/10.1007/978-3-319-61572-1_19
Tiwari, T., Tiwari, T. and Tiwari, S., 2018. How Artificial Intelligence, Machine Learning and Deep Learning are Radically Different?. International Journal of Advanced Research in Computer Science and Software Engineering, 8(2), p.1. ISSN: 2277-128X
Zhong, Haoxi, et al. "Legal judgment prediction via topological learning." Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing. 2018. https://doi.org/10.18653/v1/D18-1390
Zhong, Haoxi, et al. "How does NLP benefit legal system: A summary of legal artificial intelligence." arXiv preprint arXiv:2004.12158 (2020)
Ye, Hai, et al. "Interpretable charge predictions for criminal cases: Learning to generate court views from fact descriptions." arXiv preprint arXiv:1802.08504 (2018)
World Bank, sbhupatiraju@worldbank.org.↩︎
Toulouse School of Economics, Institute for Advanced Study, daniel.chen@iast.fr (corresponding author).↩︎
World Bank, kannanv93@gmail.com.↩︎